Prova sobre sistema linear 2º A

Para visualizar a prova clique na imagem abaixo.

Lista 04 sistema linear

Clique na imagem abaixo para visualizar ou fazer o download da lista de exercício.

lista 03 do sistema lineares

Clique na imagem abaixo para visualizar ou baixar a lista do exercício

Lista 02 de sistemas lineares

Clique na imagem abaixo para visualizar e/ou efetuar o download da lista de exercícios.

Lista 01 de sistemas lineares

 Clique na imagem abaixo para visualizar e/ou baixar a lista de exercícios.

Solução

Clique nas imagens para visualizar as soluções das atividades sobre determinantes.

Lista_2 sobre determinantes

Clique na imagem abaixo para visualizar e baixar a lista_2 de exercícios sobre determinantes.

Lista de exercícios sobre determinantes.

Clique na imagem abaixo para visualizar e baixar a lista de exercícios.

Lista - Revisão de matrizes

Clique na imagem abaixo para visualizar ou baixar a lista de exercícios.

Lista de exercícios - Multiplicação de matrizes

Clique na imagem abaixo para visualizar ou baixar a lista de exercícios.

Multiplicação de matrizes

Multiplicação de número real por matriz

Dada uma matriz A = (a_ij)_mxn e um número real k, denomina-se matriz  produto do numero real K por A, a matriz obtida multiplicando-se cada um dos seus elementos por k.

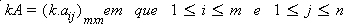
Observe como exemplo a determinação da matriz 3ª, a partir de

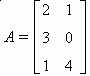
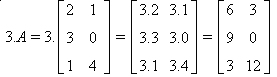
Sendo A, B, C, O (matriz nula) matrizes de mesmo tipo, valem as propriedades da multiplicação de numero real por matriz:

* 1.A = A
* (-1).A = -A
* p.O = O
* 0.A = 0
* p.(A + B) = p.A + p.B
* (p + q).B = p.B + q.B
* p.(q.A) = (p.q).A

Multiplicação de matrizes

Sendo A uma matriz do tipo mxn e B uma matriz do tipo nxp, define-se produto da matriz A pela matriz B a matriz C, do tipo mxp, tal que cada elemento de C (cij) satisfaz:

Em outras palavras, cada elemento de C é calculado multiplicando-se ordenadamente os elementos da linha i da matriz A pelos elementos correspondentes da coluna j da matriz B e , a seguir, somando-se os produtos obtidos. Veja abaixo:

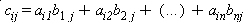
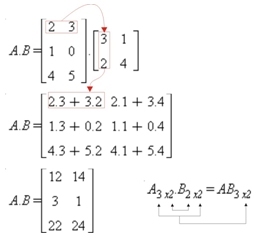
O produto entre duas matrizes A e B é definido se , e somente se, o número de colunas da matriz A for igual ao numero de linhas da matriz B. Assim:

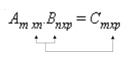
O elemento neutro da multiplicação de matrizes é a matriz identidade(I).

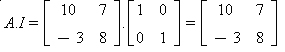
Propriedades

• Multiplicação de matrizes não é em geral comutativa, ou seja, AB ≠ BA(exceto em casos especiais). Eis um exemplo:

• Embora multiplicação de matrizes não seja comutativa, os determinantes de AB e BA são sempre iguais (se A e B são matrizes quadradas de dimensões iguais). Veja o artigo sobre determinantes para esclarecimento.
• O produto é associativo, ou seja:

• O produto distribui sob a soma:

• Propriedade de matrizes transpostas: .

Extraído de http://www.infoescola.com/matematica/operacoes-com-matrizes-multiplicacao/

http://pt.wikipedia.org/wiki/Produto_de_matrizes

Sistemas Lineares 2x2

Resolução de um sistema 2x2

Resolver um sistema linear 2 × 2 significa obter o conjunto solução do sistema.

Os dois métodos mais utilizados para a resolução de um sistema linear 2 × 2 são o método da substituição e o método da adição.

Para exemplificar, vamos resolver o sistema 2 × 2 abaixo usando os dois métodos citados.



1) Método da Substituição:



Da equação (II), obtemos x = y –1, que substituímos na equação (I)

2(y – 1) + 2 · (3) = 8 5 y = 10 y =2

Fazendo y = 2 na equação (I), por exemplo, obtemos:

2x + 3 = 8 2x = 2 x = 1

Assim: S = {(1, 2)}

2) Método da Adição:





Multiplicamos a equação II por 3 e a adicionamos, membro a membro, com a equação I.



Fazendo x = 1 na equação (I), por exemplo, obtemos:

2 · 1 + 3y = 8 y = 2

Assim: S = {(1, 2)}


Discussão de um sistema linear


O sistema linear consiste na relação mútua entre duas ou mais equações, ou seja, equações que compartilham da mesma solução ou do mesmo conjunto solução. Com esse fato surgem as classificações quanto aos conjuntos, sendo elas: Sistema Possível Determinado (apenas uma solução), Sistema Possível Indeterminado (várias soluções), Sistema Impossível (nenhuma solução).












Referências bibliográficas:

http://interna.coceducacao.com.br/ebook/pages/1795.htm acesso em 19/02/2013.

http://www.brasilescola.com/matematica/discussao-analise-sistema-linear.htm acesso em 19/02/2013.

http://www.slideshare.net/AngelicaBrasil/anlise-grfica-de-sistemas-lineares acesso em 19/02/2013

Determinantes

Matriz de ordem 1


O determinante de uma matriz quadrada de ordem 1 é o valor do próprio elemento.


Matriz de ordem 2

Dada a matriz A de ordem dois A = , o seu determinante será calculado da seguinte forma:

O determinante de ordem dois possui uma diagonal principal e uma diagonal secundária.



O cálculo do seu valor numérico é feito pela diferença do produto da diagonal principal com o produto da diagonal secundária.

det A = = - 3 – (- 10) = - 3 + 10 = 7


Matriz de ordem 3

Dada a matriz de ordem 3, B = o valor numérico do seu determinante é calculado da seguinte forma:

Primeiro representamos essa matriz em forma de determinante e repetimos as duas primeiras colunas.

det B =

Depois calculamos os produtos das diagonais principais e os produtos das diagonais secundárias.

det B =

Deve-se pegar o oposto dos produtos das diagonais secundárias e somar com os produtos das diagonais principais.

Det B = 0 – 40 + 0 – 15 + 0 – 4 = -59

Essa regra utilizada no cálculo do determinante de matriz de ordem 3 é chamada de Regra de Sarrus.


Propriedades dos determinantes

Em todas as situações abaixo, consideraremos matrizes quadradas de ordem n>2


1.0 Se In é a matriz identidade, então: det(In) = 1

2.0 Se N é uma matriz nula, então: det(N) = 0

3.0 Se uma linha (ou coluna) da matriz A for nula, então: det(A) = 0

4.0 A matriz A bem como a sua transposta At, possuem o mesmo determinante de A, isto é: det(At) = det(A)

5.0 Se B é a matriz obtida pela multiplicação de uma linha (ou coluna) da matriz A por um escalar k, então: det(B) = k det(A)

6.0 Se B é a matriz obtida pela troca de duas linhas (ou colunas) de A, então: det(B) = - det(A)

7.0 Se A tem duas linhas (ou colunas) iguais, então: det(A) = 0

8.0 Se a diferença entre os elementos de duas linhas (ou colunas) de uma matriz A é uma mesma constante, então: det(A) = 0

9.0 Se uma linha (ou coluna) de A for múltipla de uma outra linha (ou coluna) de A, então: det(A) = 0

10.0 Se A é uma matriz triangular, então: det(A) é igual ao produto de sua diagonal principal.


Referências bibliográficas:

http://www.mundoeducacao.com.br/matematica/determinante-matriz-ordem-1-2-ou-3.htm acesso em 19/02/2013

http://pessoal.sercomtel.com.br/matematica/medio/matrizes/determinantes.htm acesso em 19/02/2013

http://www.colegioweb.com.br/matematica/matriz-de-ordem-2.html acesso em 19/02/2013

Matrizes - Lei de formação

Lei de formação de uma matriz 

     Toda matriz pode ser declarada através de uma lei de formação para seus elementos que consiste numa função ordinal de duas variáveis. Estas variáveis assumem os valores dos índices que designam a posição (linha e coluna) de cada elemento da matriz. Assim, obtemos o valor de um elemento aij de uma matriz Am×n calculando a imagem da função no ponto (i, j), ou seja, aij = f( i , j ). 

     A sentença que declara uma matriz de forma condensada usando as funções ordinais pode parecer assustadora, por isso vamos observá-la com calma: 

A = (aij )mxn  tal que aij  = f( i , j )

     Primeiro lemos a letra que designa o nome da matriz: A. Depois, entre os parênteses a letra a que designa cada um dos os elementos da matriz. Esta última vem acompanhada de dois índices algébricos  i e  j que indicam respectivamente a linha e a coluna de um elemento específico. Do lado de fora do parêntese, há um outro índice composto por dois números  m e  n que indicam o formato da matriz. Desta forma devemos tomar  i e  j como variáveis ordinais cujos valores máximos são respectivamente m e n. 

     Isso tudo serve para definir o formato da matriz, ou seja, quantas são suas linhas e suas colunas, além de apresentar as letras que indicarão as posições específicas de cada elemento, neste caso i e j, pois elas serão tomadas como variáveis na função f (lei de formação) que expressa cada elemento da matriz em função dos números que representam a linha e a coluna em que este elemento se situa. 
     Sendo I o conjunto dos números naturais de 1 até m e J o conjunto dos naturais de 1 até n temos que o domínio da função f é o produto cartesiano I×J, ou seja, o conjunto de todos os pares ordenados de números naturais cuja abscissa varia de 1 a m e a ordenada varia de 1 a n. Finalmente, a matriz A consiste numa apresentação organizada da imagem da função f na forma de uma tabela.


Exemplos:

Podemos construir uma matriz de acordo com uma lei de formação baseada em situações variadas. Por exemplo, vamos construir uma matriz de ordem 3 x 3, seguindo a orientação a_ij = 3i + 2j.

 Vamos escrever a matriz B dada por (a_ij)4x4, de modo que i + j, se i = j e i – j, se i ≠ j.

Extraído de :

http://www.matematiao.com.br/site/wp-content/uploads/2012/07/%C3%81lgebra-linear.pdf acesso em 19/02/2013

http://www.brasilescola.com/matematica/matriz.htm acesso em 19/02/2013

Matrizes - Adição e Subtração

Adição

Para adicionarmos duas ou mais matrizes é preciso que todas elas tenham o mesmo número de linhas e de colunas. A soma dessas matrizes irá resultar em outra matriz que também terá o mesmo número de linhas e de colunas.
Os termos deverão ser somados com os seus termos correspondentes.
Concluímos que: 

Dada duas matrizes, A e B, as duas de ordem m x n. Então, A + B = C, com C de ordem m x n ↔ a11 + b11 = c11.

Veja o exemplo abaixo:
Dado a matriz A = e matriz B = , se efetuarmos a soma dessas matrizes teremos:

Somaremos os termos correspondentes em cada matriz:


Com a soma das duas matrizes obtivemos outra matriz C = .

Propriedades da Adição

Sendo ,  e  matrizes do mesmo tipo (), temos as seguintes propriedades para a adição:

a) comutativa: 
b) associativa: () + C = A + (B + C)
c) elemento neutro: , sendo  a matriz nula 
d) elemento oposto: 

Subtração

Para efetuarmos a subtração de duas matrizes, as matrizes subtraídas devem ter a mesma ordem (mesmo número de linhas e colunas) e a matriz obtida com a subtração (matriz diferença) também deve ter o mesmo número de linhas e colunas que as matrizes subtraídas.
Cada elemento de uma matriz deve ser subtraído com o elemento correspondente da outra matriz.
Concluímos que:

Dada duas matrizes, A e B, as duas de ordem m x n. Então A – B = C de ordem m x n ↔ a11 – a11 = c11

Veja o exemplo abaixo:
Dada a matriz A = e a matriz B = , se efetuamos a subtração dessas matrizes, temos: 

Subtraindo os termos correspondentes das matrizes:

Com a subtração das duas matrizes obtivemos uma matriz C =


Referências:
http://www.mundoeducacao.com.br/matematica/adicao-subtracao-matrizes.htm acesso em 19/02/2013.
http://www.mundofisico.joinville.udesc.br/PreVestibular/2005-1/mod1/node51.html acesso em 19/02/2013